Trong thống kê và phân tích dữ liệu, việc chỉ nhìn vào giá trị trung bình đôi khi chưa đủ để phản ánh hết đặc điểm của một tập số liệu. Chúng ta cần thêm một thước đo để biết dữ liệu ổn định hay biến động nhiều, và đó chính là độ lệch chuẩn. Vậy độ lệch chuẩn là gì, công thức tính ra sao và ý nghĩa của nó trong thực tiễn như thế nào? Hãy cùng tìm hiểu chi tiết qua nội dung dưới đây.
1. Độ lệch chuẩn là gì?
Độ lệch chuẩn (tiếng Anh: Standard Deviation, ký hiệu: σ cho tổng thể, s cho mẫu) là một thước đo thống kê thể hiện mức độ phân tán hoặc biến thiên của các giá trị trong một tập dữ liệu so với giá trị trung bình. Nói cách khác, nó cho biết các giá trị trong tập dữ liệu nằm gần hay xa giá trị trung bình.

Độ lệch chuẩn là gì?
>> Đọc thêm: Chủ thể quản lý nhà nước là gì?
2. Công thức tính độ lệch chuẩn
Về cơ bản, công thức tính độ lệch chuẩn phụ thuộc vào việc bạn đang tính cho tổng thể (population) hay mẫu (sample). Do đó, trong xác suất thống kê sẽ có hai cách tính độ lệch chuẩn, tương ứng với hai trường hợp:
2.1. Công thức tính độ lệch chuẩn tổng thể
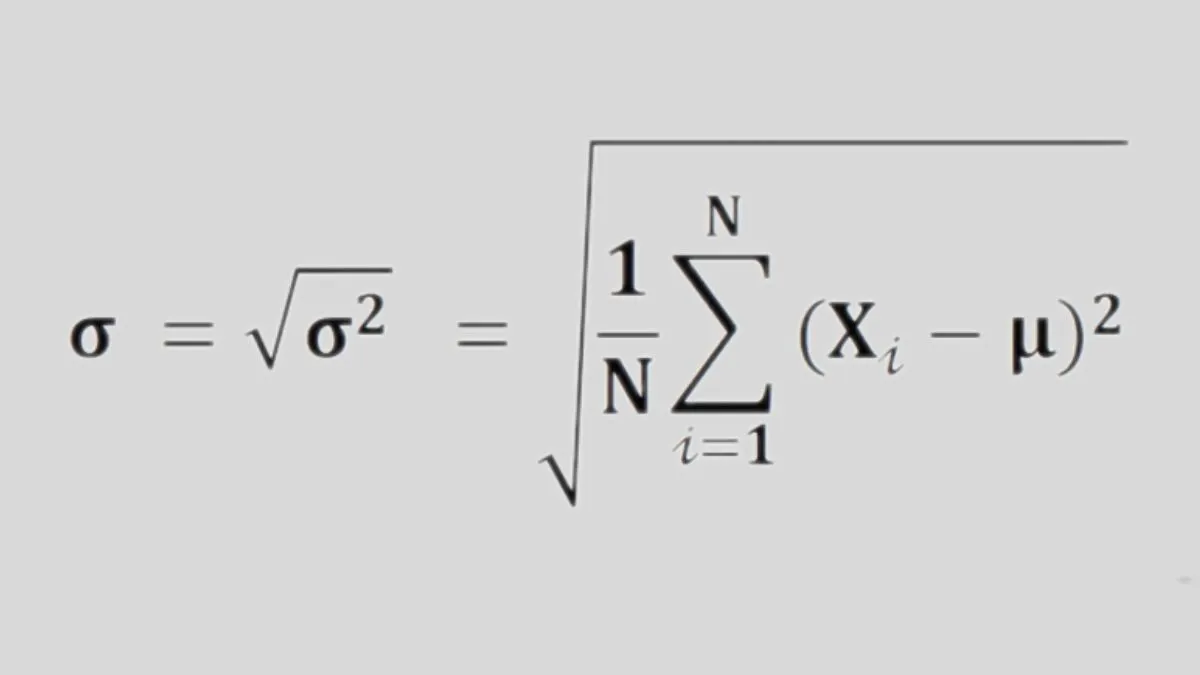
Công thức tính độ lệch chuẩn tổng thể
Trong đó:
- σ (sigma): độ lệch chuẩn tổng thể
- N: kích thước toàn bộ tổng thể
- xᵢ: từng giá trị dữ liệu
- μ (mu): giá trị trung bình tổng thể
2.2. Công thức tính độ lệch chuẩn cho mẫu
Độ lệch chuẩn (S) của một tập dữ liệu được tính bằng công thức sau:
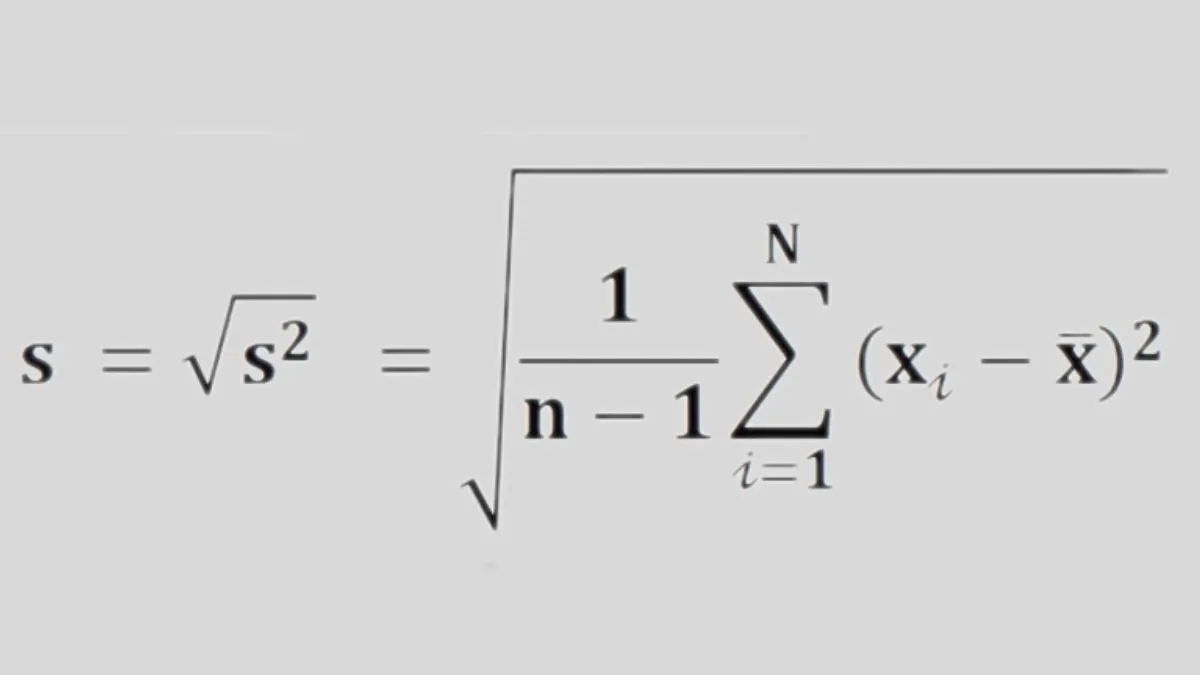
Công thức tính độ lệch chuẩn cho mẫu
Trong đó:
- S: Độ lệch chuẩn
- xᵢ: Giá trị quan sát thứ i
- x̅: Giá trị trung bình
- N: Số phần tử trong mẫu
3. Các bước tính độ lệch chuẩn

Các bước tính độ lệch chuẩn
Để dễ hiểu, hãy cùng tính độ lệch chuẩn qua ví dụ sau:
Giả sử ta có tập dữ liệu gồm 5 số: 2, 4, 6, 8, 10.
Bước 1: Tính giá trị trung bình (x̅)
x̅ = (2 + 4 + 6 + 8 + 10) / 5 = 6
Bước 2: Tính tổng bình phương các độ lệch
Σ(xᵢ – x̅)² = 16 + 4 + 0 + 4 + 16 = 40
Bước 3: Tính phương sai
40 / 5 = 8
Bước 4: Tính độ lệch chuẩn
√8 = 2.83
Vậy, độ lệch chuẩn (S) của tập dữ liệu là 2.83.
Trong thực tế, ta thường làm tròn độ lệch chuẩn đến hai chữ số thập phân. Do đó, độ lệch chuẩn của tập dữ liệu trong ví dụ này là 2.83 ≈ 2.
>> Tham khảo thêm: Dịch vụ làm luận văn tiết kiệm chi phí, hiệu quả vượt trội
4. Cách tính độ lệch chuẩn trong Excel
Trong Excel, bạn có thể tính độ lệch chuẩn bằng cách sử dụng hàm STDEV. Hãy làm theo các bước sau:
- Chọn ô mà bạn muốn hiển thị kết quả.
- Nhập hàm =STDEV (number1,[number2],…)
- Chọn các ô chứa giá trị trong tập dữ liệu hoặc nhập các giá trị tương ứng vào hàm STDEV.
- Đóng ngoặc và nhấn Enter.

Cách tính độ lệch chuẩn trong Excel
Ví dụ: Cho tập dữ liệu gồm 5 số: 2, 4, 6, 8, 10. Bạn cần tính độ lệch chuẩn của tập dữ liệu này.
- Nhập trực tiếp các giá trị trong tập dữ liệu vào hàm STDEV như sau: =STDEV (2, 4, 6, 8, 10)
- Hoặc nhập chọn các ô chứa các giá trị trong tập dữ liệu như sau: =STDEV (A1:A5)
- Kết quả sẽ hiển thị là 3.16, tương tự như kết quả tính bằng công thức ở trên.
5. Ý nghĩa của độ lệch chuẩn
- Đo lường mức độ phân tán của dữ liệu so với giá trị trung bình: độ lệch chuẩn càng lớn → dữ liệu càng phân tán; độ lệch chuẩn nhỏ → dữ liệu tập trung gần trung bình.
- Phản ánh mức độ biến động của dữ liệu: độ lệch chuẩn thấp cho thấy dữ liệu ổn định; độ lệch chuẩn cao thể hiện dữ liệu thay đổi mạnh.
- Là căn bậc hai của phương sai, giúp mô tả mức độ chênh lệch giữa các giá trị với giá trị trung bình trong bất kỳ tập dữ liệu nào.
- Công cụ quan trọng trong đầu tư – giao dịch tài chính: giúp đo lường sự biến động của giá, đánh giá mức độ rủi ro và dự đoán xu hướng thị trường.
- Trong SPSS, độ lệch chuẩn thể hiện mức độ khác biệt giữa các câu trả lời của đáp viên: độ lệch chuẩn nhỏ → các đáp viên trả lời khá giống nhau; độ lệch chuẩn lớn → câu trả lời đa dạng, khác biệt nhiều.
- Giúp đánh giá cấu trúc dữ liệu: cho biết giá trị có tập trung (ít phân tán) hay phân tán mạnh (xa trung bình).

Độ lệch chuẩn giúp đánh giá sự ổn định của dữ liệu
Tóm lại, độ lệch chuẩn chính là thước đo quan trọng giúp chúng ta biết dữ liệu có ổn định hay biến động. Khi nắm rõ khái niệm, công thức tính và ý nghĩa của nó, bạn sẽ dễ dàng áp dụng vào học tập, nghiên cứu cũng như công việc thực tiễn. Hiểu đúng về độ lệch chuẩn cũng chính là bước đầu để phân tích dữ liệu khoa học và hiệu quả hơn.


 14 Tháng 1, 2026
14 Tháng 1, 2026 Share
Share










