Công thức tính độ lệch chuẩn chính xác

Độ lệch chuẩn là một thước đo quan trọng trong thống kê, được sử dụng để đo lường sự phân tán của dữ liệu xung quanh giá trị trung bình. Nó cho biết mức độ biến động của các điểm dữ liệu so với trung bình, và được sử dụng rộng rãi trong nhiều lĩnh vực như kinh doanh, khoa học và kỹ thuật. Bài viết này sẽ hướng dẫn bạn cách tính chi tiết từ công thức tính độ lệch chuẩn và hiểu rõ hơn về độ lệch chuẩn trong toán học và áp dụng vào đời sống hàng ngày.

Độ lệch chuẩn là gì?

Độ lệch chuẩn là căn bậc hai của phương sai, một phép đo phổ biến dùng để mô tả sự phân tán của dữ liệu xung quanh giá trị trung bình (trung bình). Nói cách khác, độ lệch chuẩn cho biết trung bình mỗi điểm dữ liệu cách xa trung bình bao nhiêu đơn vị.

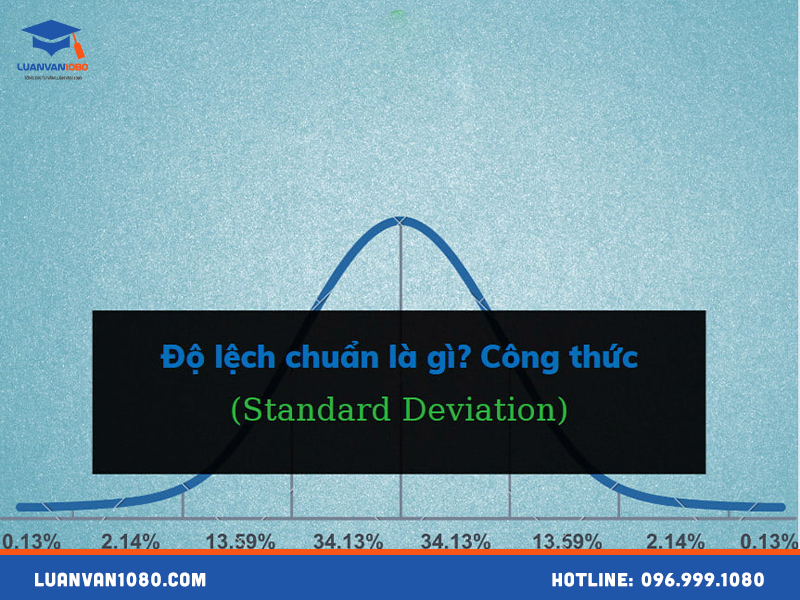
Ngoài ra, bạn có thể tìm hiểu thêm về phương sai để hiểu thêm về mối liên hệ của 2 khái niệm này.

Ý nghĩa của độ lệch chuẩn

Độ lệch chuẩn có ý nghĩa quan trọng trong nhiều lĩnh vực, bao gồm:

• Phân tích dữ liệu: Độ lệch chuẩn giúp đánh giá sự phân tán của dữ liệu và xác định mức độ biến động của các điểm dữ liệu.
• Kiểm tra giả thuyết: Độ lệch chuẩn được sử dụng để tính toán các khoảng tin cậy và kiểm tra giả thuyết thống kê.
• Dự báo: Độ lệch chuẩn có thể được sử dụng để dự báo giá trị tương lai của dữ liệu dựa trên mô hình thống kê.

Ví dụ minh họa về độ lệch chuẩn

Hãy xem xét hai tập dữ liệu sau:

• Tập dữ liệu A: 10, 12, 14, 16, 18
• Tập dữ liệu B: 5, 10, 15, 20, 25

Cả hai tập dữ liệu đều có trung bình là 14. Tuy nhiên, độ lệch chuẩn của tập dữ liệu A là 3.16, trong khi độ lệch chuẩn của tập dữ liệu B là 6.71. Điều này cho thấy rằng các điểm dữ liệu trong tập dữ liệu B phân tán rộng hơn so với tập dữ liệu A.

Công thức tính độ lệch chuẩn

Công thức chung để tính độ lệch chuẩn (s) của mẫu là:

s = √[∑(xᵢ - x̄)² / (n - 1)]

Trong đó:

• xᵢ: Giá trị của điểm dữ liệu thứ i
• x̄: Giá trị trung bình của mẫu
• n: Số lượng điểm dữ liệu trong mẫu
• ∑: Ký hiệu tổng

Cách tính độ lệch chuẩn theo từng bước

Dưới đây là các bước để tính độ lệch chuẩn của một mẫu dữ liệu:

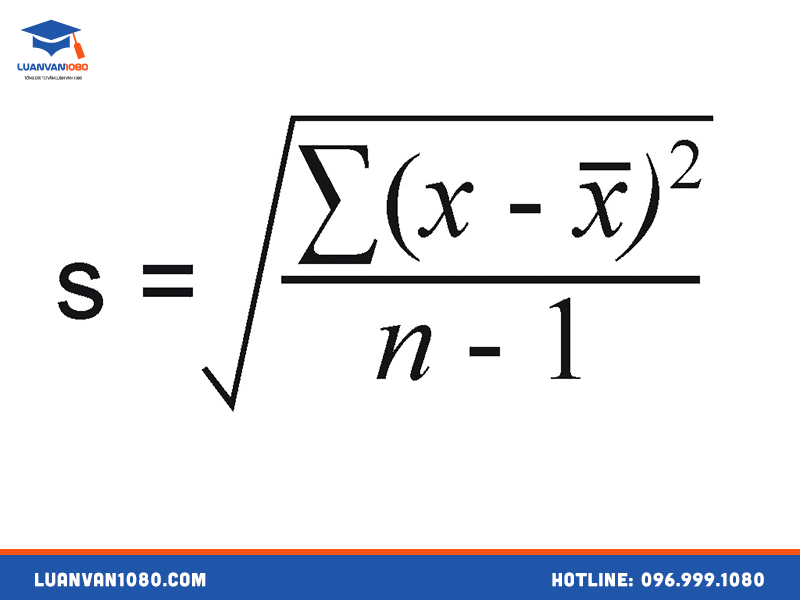
• Tính giá trị trung bình (x̄) của mẫu: Cộng tất cả các giá trị trong mẫu và chia cho số lượng điểm dữ liệu.
• Tính độ lệch của mỗi điểm dữ liệu so với trung bình (xᵢ - x̄): Trừ giá trị trung bình khỏi mỗi điểm dữ liệu.
• Bình phương mỗi độ lệch (xᵢ - x̄)²: Bình phương mỗi kết quả từ bước 2.
• Cộng tất cả các giá trị bình phương (∑(xᵢ - x̄)²): Cộng tất cả các kết quả từ bước 3.
• Chia tổng các giá trị bình phương cho (n - 1): Chia kết quả từ bước 4 cho (n - 1), nơi n là số lượng điểm dữ liệu.
• Tính căn bậc hai của kết quả: Tính căn bậc hai của kết quả từ bước 5 để tìm độ lệch chuẩn (s).

Ví dụ minh họa về cách tính độ lệch chuẩn

Hãy tính độ lệch chuẩn của tập dữ liệu sau: 5, 10, 15, 20, 25

• Tính giá trị trung bình (x̄): (5 + 10 + 15 + 20 + 25) / 5 = 15
• Tính độ lệch của mỗi điểm dữ liệu so với trung bình (xᵢ - x̄):
• 5 - 15 = -10
• 10 - 15 = -5
• 15 - 15 = 0
• 20 - 15 = 5
• 25 - 15 = 10
• Bình phương mỗi độ lệch (xᵢ - x̄)²:
• (-10)² = 100
• (-5)² = 25
• 0² = 0
• 5² = 25
• 10² = 100
• Cộng tất cả các giá trị bình phương (∑(xᵢ - x̄)²): 100 + 25 + 0 + 25 + 100 = 250
• Chia tổng các giá trị bình phương cho (n - 1): 250 / (5 - 1) = 62.5
• Tính căn bậc hai của kết quả: √62.5 = 7.91

Độ lệch chuẩn của tập dữ liệu này là 7.91. 

Phương sai và độ lệch chuẩn thường được sử dụng khá phổ biến trong các công việc tính toán hiện nay. Việc hiểu rõ về cả 2 khái niệm này sẽ giúp việc tính toán được nhanh chóng và dễ dàng hơn.

Ứng dụng trong các phép tính xác suất

Độ lệch chuẩn được sử dụng rộng rãi trong các phép tính xác suất, đặc biệt là khi làm việc với phân phối chuẩn.

• Quy tắc đã kiểm chứng (Empirical Rule): Phân phối chuẩn cho thấy khoảng 68% dữ liệu nằm trong khoảng một độ lệch chuẩn từ trung bình, khoảng 95% dữ liệu nằm trong khoảng hai độ lệch chuẩn từ trung bình và khoảng 99.7% dữ liệu nằm trong khoảng ba độ lệch chuẩn từ trung bình.
• Khoảng tin cậy: Độ lệch chuẩn được sử dụng để xây dựng khoảng tin cậy, là một phạm vi giá trị có khả năng chứa giá trị thực của tham số dân số.
• Kiểm tra giả thuyết: Độ lệch chuẩn được sử dụng để tính toán thống kê kiểm tra, dùng để kiểm tra các giả thuyết về phân phối dữ liệu.

Độ lệch chuẩn trong các phép tính thực tế

Độ lệch chuẩn được ứng dụng nhiều trong các phép tính thực tế, ví dụ:

• Tài chính: Độ lệch chuẩn được sử dụng để đánh giá mức độ rủi ro của các khoản đầu tư, bao gồm cả cổ phiếu và trái phiếu.
• Nghiên cứu thị trường: Độ lệch chuẩn được sử dụng để phân tích kết quả khảo sát và đánh giá độ tin cậy của dữ liệu.
• Khoa học: Độ lệch chuẩn được sử dụng để phân tích kết quả thí nghiệm và xác định độ chính xác của các phép đo trong các đề tài nghiên cứu khoa học.

Độ lệch chuẩn là một phép đo quan trọng trong thống kê, cung cấp thông tin về sự phân tán của dữ liệu xung quanh giá trị trung bình. Việc hiểu rõ khái niệm và công thức tính độ lệch chuẩn là cần thiết để áp dụng nó hiệu quả trong phân tích định lượng, kiểm tra giả thuyết và xây dựng mô hình thống kê. Ngoài ra, khi sử dụng độ lệch chuẩn, cần lưu ý đến việc giải thích ý nghĩa của nó trong ngữ cảnh của dữ liệu và mục tiêu phân tích.

Liên hệ dịch vụ phân tích định lượng giá tốt theo yêu cầu

Bạn đang tìm kiếm dịch vụ phân tích định lượng chất lượng cao với mức giá phải chăng? Hãy liên hệ ngay với Luận Văn 1080 để được tư vấn và báo giá miễn phí. Chúng tôi cung cấp dịch vụ phân tích số liệu chuyên nghiệp, tùy chỉnh theo yêu cầu cụ thể của từng khách hàng. 

Đội ngũ chuyên gia giàu kinh nghiệm của Luận Văn 1080 sẽ hỗ trợ bạn từ khâu thiết kế nghiên cứu đến phân tích và diễn giải kết quả. Đừng bỏ lỡ cơ hội nâng cao chất lượng nghiên cứu của bạn với mức chi phí tối ưu nhất. Hãy gọi ngay cho chúng tôi hoặc để lại thông tin liên hệ để nhận được tư vấn chi tiết về dịch vụ phân tích định lượng tại Luận Văn 1080.

Thông tin liên hệ:

• Hotline: 096 999 1080
• Email: luanvan1080@gmail.com
• Địa chỉ: 

275 Nguyễn Trãi – Thanh Xuân – Hà Nội

25 Tiên Sơn 15 - Hòa Cường Nam - Hải Châu - Đà Nẵng

16 Đường B2 - KDC Hưng Phú 1 - Cái Răng - Cần Thơ

35 Lê Văn Chí - Phường Linh Trung - Thủ Đức - TPHCM