Phương sai và độ lệch chuẩn có khác nhau không?

Việc hiểu rõ về phương sai và độ lệch chuẩn là rất quan trọng trong thống kê, được sử dụng để đánh giá sự biến thiên và tập trung của dữ liệu. Những khái niệm này có vai trò quan trọng trong việc phân tích và đưa ra kết luận trong nghiên cứu khoa học, đặc biệt là những nghiên cứu liên quan đến định tính. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về ý nghĩa và cách tính toán của phương sai và độ lệch chuẩn, cũng như sự khác biệt giữa hai khái niệm này.

Phương sai (variance)

Ý nghĩa của phương sai

Phương sai (variance) là một đại lượng đo lường sự biến thiên của dữ liệu so với giá trị trung bình. Nó cho biết mức độ phân tán của các giá trị xung quanh giá trị trung bình.

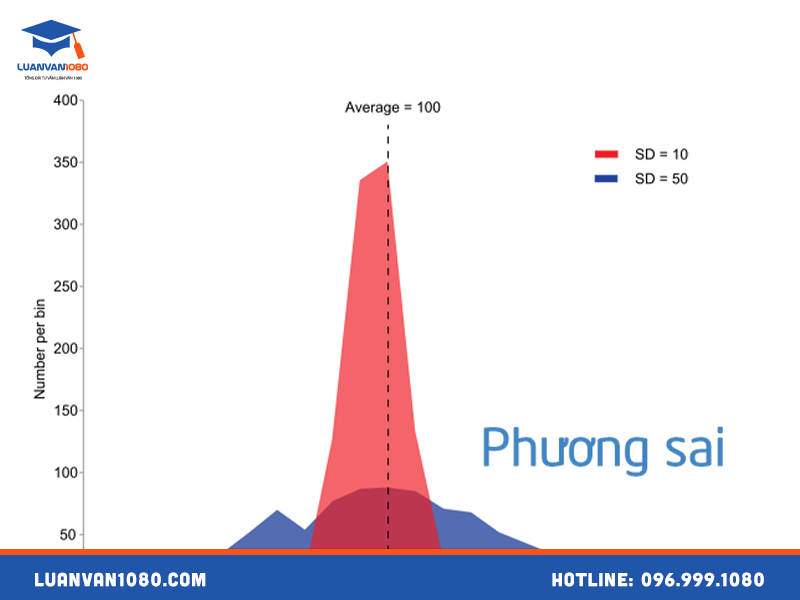
Đơn giản hơn, phương sai là sự khác biệt giữa giá trị thực tế và giá trị trung bình của tập dữ liệu. Nếu phương sai càng lớn, thì sự biến thiên của dữ liệu càng lớn, ngược lại, nếu phương sai nhỏ, thì sự biến thiên của dữ liệu cũng nhỏ.

Công thức tính toán phương sai

Để tính toán phương sai, chúng ta sử dụng công thức sau: σ² = Σ (xi - x̄)² / n

Trong đó, n là số lượng các giá trị trong tập dữ liệu, xᵢ là giá trị của một quan sát bất kỳ, và x̄ là giá trị trung bình của tập dữ liệu. Khi tính toán phương sai, chúng ta cần lấy bình phương của độ lệch của từng giá trị so với giá trị trung bình, sau đó tính trung bình của các bình phương này.

Ví dụ, ta có tập dữ liệu sau: 5, 8, 6, 7, 10. Ta có thể tính được giá trị trung bình của tập dữ liệu này là (5+8+6+7+10)/5 = 7.2. Tiếp theo, ta tính độ lệch của từng giá trị so với giá trị trung bình: -2.2, 0.8, -1.2, -0.2, 2.8. Sau đó, ta lấy bình phương của các độ lệch này: 4.84, 0.64, 1.44, 0.04, 7.84. Cuối cùng, ta tính trung bình của các bình phương này: (4.84+0.64+1.44+0.04+7.84)/5 = 3.56. Vậy phương sai của tập dữ liệu này là 3.56.

Ví dụ về sử dụng phương sai trong nghiên cứu khoa học

Để hiểu rõ hơn về ý nghĩa của phương sai, chúng ta có thể xem xét một ví dụ trong đề tài nghiên cứu khoa học về hiệu quả của một loại thuốc mới. Trong thí nghiệm này, nhóm nghiên cứu đã chọn ngẫu nhiên 100 người bệnh và chia thành hai nhóm, một nhóm được điều trị bằng thuốc mới và một nhóm không được điều trị. Kết quả cuối cùng cho thấy, nhóm được điều trị bằng thuốc mới có tỷ lệ hồi phục cao hơn so với nhóm không được điều trị. Tuy nhiên, để có thể kết luận rằng thuốc mới thực sự hiệu quả, chúng ta cần phải xem xét đến sự biến thiên của kết quả điều trị trong từng nhóm.

Nếu phương sai của kết quả điều trị ở hai nhóm là như nhau, thì có thể kết luận rằng thuốc mới đã có hiệu quả. Tuy nhiên, nếu phương sai của nhóm được điều trị bằng thuốc mới lớn hơn so với nhóm không được điều trị, thì chúng ta có thể nghi ngờ rằng sự khác biệt trong tỷ lệ hồi phục giữa hai nhóm có thực sự do thuốc mới hay không. Do đó, sử dụng phương sai giúp chúng ta đánh giá sự biến động của kết quả nghiên cứu và đưa ra kết luận chính xác hơn.

Độ lệch chuẩn (standard deviation)

Ý nghĩa của độ lệch chuẩn

Độ lệch chuẩn là một đại lượng đo lường sự biến động của dữ liệu trong một tập hợp. Nó cho biết mức độ phân tán của dữ liệu so với giá trị trung bình, tương tự như phương sai. Tuy nhiên, độ lệch chuẩn được tính bằng cách lấy căn bậc hai của phương sai, điều này giúp chúng ta có thể đo lường sự biến động theo cùng đơn vị với dữ liệu ban đầu. Đơn vị của độ lệch chuẩn là đơn vị của dữ liệu.

Công thức tính toán độ lệch chuẩn

Để tính toán độ lệch chuẩn, chúng ta sử dụng công thức sau: s = √σ²

Trong đó, s là độ lệch chuẩn và được tính bằng cách lấy căn bậc hai của phương sai. Công thức này cũng tương tự như công thức tính toán phương sai, chỉ khác là ta thay đổi từ tính bình phương sang lấy căn bậc hai.

Ví dụ về sử dụng độ lệch chuẩn trong nghiên cứu khoa học

Tiếp tục ví dụ về hiệu quả của thuốc mới trong điều trị bệnh nhân, chúng ta có thể sử dụng độ lệch chuẩn để đánh giá sự biến động của kết quả điều trị ở hai nhóm. Nếu độ lệch chuẩn của kết quả điều trị ở nhóm được điều trị bằng thuốc mới nhỏ hơn so với nhóm không được điều trị, thì chúng ta có thể kết luận rằng độ tin cậy của kết quả nghiên cứu cao hơn. 

Tuy nhiên, nếu độ lệch chuẩn của nhóm được điều trị bằng thuốc mới lớn hơn so với nhóm không được điều trị, thì chúng ta cần kiểm tra lại sự khác biệt trong tỷ lệ hồi phục giữa hai nhóm.

Sự khác biệt giữa phương sai và độ lệch chuẩn

Phương sai và độ lệch chuẩn là hai khái niệm liên quan đến sự biến thiên của dữ liệu. Tuy nhiên, chúng có những điểm khác biệt sau:

• Đơn vị: Phương sai không có đơn vị, trong khi độ lệch chuẩn có đơn vị. Do đó, độ lệch chuẩn cho ta biết được mức độ biến động của dữ liệu theo cùng đơn vị với dữ liệu ban đầu.

• Giá trị tối đa: Phương sai có thể có giá trị bất kỳ, trong khi độ lệch chuẩn có giá trị không âm. Điều này giúp chúng ta dễ dàng so sánh độ biến thiên giữa các tập dữ liệu khác nhau.

• Ảnh hưởng của outlier: Một outlier (giá trị ngoại lệ) có thể làm tăng đáng kể phương sai, nhưng không ảnh hưởng nhiều đến độ lệch chuẩn. Do đó, khi tính toán độ biến động của dữ liệu, ta có thể sử dụng độ lệch chuẩn thay vì phương sai để tránh ảnh hưởng của outlier.

Hy vọng bài viết đã giúp bạn hiểu rõ hơn về phương sai và độ lệch chuẩn và áp dụng chúng một cách chính xác trong nghiên cứu của mình.

Liên hệ với đơn vị phân tích định lượng theo yêu cầu

Bạn đang gặp khó khăn trong việc phân tích dữ liệu SPSS của mình? Bạn đang tìm kiếm một đơn vị uy tín để hỗ trợ phân tích định lượng, đảm bảo kết quả nghiên cứu của bạn chính xác và đáng tin cậy? Đừng chần chừ nữa, hãy liên hệ ngay với Luận Văn 1080. Với đội ngũ chuyên gia giàu kinh nghiệm và phần mềm phân tích hiện đại, chúng tôi cam kết mang đến cho bạn dịch vụ phân tích định lượng tốt nhất, giúp luận văn của bạn đạt điểm cao.

Để được hỗ trợ tư vấn chi tiết hơn vui lòng liên hệ qua thông tin dưới đây.

Thông tin liên hệ:

• Hotline: 096 999 1080
• Email: luanvan1080@gmail.com
• Địa chỉ: 

275 Nguyễn Trãi – Thanh Xuân – Hà Nội

25 Tiên Sơn 15 - Hòa Cường Nam - Hải Châu - Đà Nẵng

16 Đường B2 - KDC Hưng Phú 1 - Cái Răng - Cần Thơ

35 Lê Văn Chí - Phường Linh Trung - Thủ Đức - TPHCM