Sai số chuẩn của hàm hồi quy đóng vai trò quan trọng trong nhiều nghiên cứu, không thể thiếu trong các quá trình tính toán, thống kê của nhiều lĩnh vực. Bên cạnh đó nó còn được hiểu như một ước tính chung dùng để đo lường giá trị thay đổi của các hệ số hồi quy giữa các mẫu trong cùng một tổng thể, khác hoàn toàn so với định nghĩa sai số chuẩn độ của hóa phân tích.
Bài viết dưới đây sẽ giúp mọi người hiểu chi tiết hơn về định nghĩa này, bên cạnh một số bí quyết giúp quá trình tính toán sai số chuẩn trở nên hiệu quả nhất, cùng xem ngay nhé. Luận Văn 1080 sẽ giúp bạn khai phá thông tin cơ bản và chi tiết cho người mới bắt đầu.
1. Khái quát về sai số chuẩn

Sai Số Chuẩn Là Gì?
1.1. Định nghĩa
Sai số chuẩn (Standard Error – SE) là một đại lượng thống kê đo lường độ lệch trung bình của các giá trị dữ liệu so với giá trị trung bình của tập dữ liệu đó. Tiêu chuẩn sai số cho phép:
- Nếu sai số chuẩn lớn: dữ liệu có xu hướng phân bố rộng và không gom vào một điểm trung tâm duy nhất nên tính chính xác không cao.
- Nếu sai số chuẩn nhỏ: dữ liệu có xu hướng gom lại gần giá trị trung bình nên tính chính xác cao.
1.2. Công thức cơ bản
Sai số chuẩn được tính bằng cách: lấy độ lệch chuẩn chia cho căn bậc hai của số cỡ mẫu.
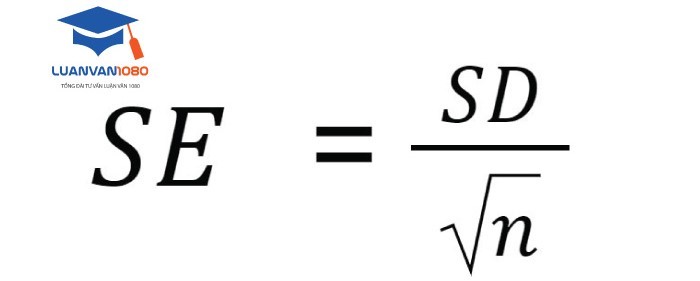
Công thức sai số chuẩn SE
Trong đó:
- SD: Độ lệch chuẩn (standard deviation) của mẫu
- n: Kích thước mẫu (số lượng quan sát được)
1.3. Mục đích
Sai số chuẩn trong hàm hồi quy được sử dụng để thể hiện độ lệch chuẩn của các dữ liệu thống kế có mẫu khác nhau như giá trị trung bình, giá trị trung vị.
Ví dụ “sai số chuẩn của giá trị trung bình”, cho thấy độ lệch chuẩn của giá trị trung bình được lấy ra từ tổng thể, sai số chuẩn nhỏ nhất sẽ đại diện cho tổng thể.
Nó thường được sử dụng trong các phép đo lường và thử nghiệm trong các trường hợp:
- Lĩnh vực khoa học
- Đánh giá chất lượng sản phẩm/dịch vụ
- Lĩnh vực kinh doanh và tài chính để đánh giá rủi ro và xác định tiềm năng lợi nhuận.
1.4. Ý nghĩa

Ý nghĩa sai số chuẩn?
Sai số chuẩn của hàm hồi quy cho biết khoảng chênh lệch giữa giá trị trung bình của tổng thể và giá trị đã biết, có nghĩa trên thực tế sẽ có nhiều giá trị tương ứng với từng thời điểm đánh giá so với giá trị trung bình trong kết quả thống kê, từ đó giúp ích cho chúng ta rất nhiều khi ghi nhận lại những kết quả cho nhiều trường hợp đo lường khác nhau.
1.5. Mở rộng công thức cho hệ số hồi quy trong mô hình thống kê
Sai số chuẩn cho hệ số hồi quy trong mô hình thống kê (ví dụ trong hồi quy tuyến tính) sẽ được tính bằng cách:
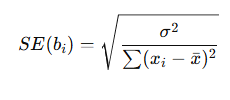
Công thức tính sai số chuẩn cho hệ số hồi quy trong mô hình thống kê
Trong đó:
bi: hệ số hồi quy ước lượng
σ2: phương sai của sai số ngẫu nhiên
xi: giá trị biến độc lập
>> Đọc thêm: Đa Cộng Tuyến Là Gì? Phương Pháp Phân Tích Và Quy Trình Thực Hiện
2. Sự khác biệt giữa sai số chuẩn và độ lệch chuẩn
Mặc dù mối quan hệ giữa sai số chuẩn và độ lệch chuẩn có sự tương đồng với nhau, nhưng chúng cũng có một số khác biệt nhất định bao gồm:
| Nội dung so sánh | Sai số chuẩn
(Standard Error – SE) |
Độ lệch chuẩn
(Standard Deviation – SD) |
| Định nghĩa | Sai số chuẩn là một phép đo độ lớn của sai lệch giữa giá trị đo và giá trị trung bình. | Độ lệch chuẩn là một phép đo độ lớn của độ lệch giữa giá trị đo và giá trị trung bình. |
| Công thức | Công thức tính sai số chuẩn là độ lệch chuẩn chia cho căn bậc hai của số lượng quan sát | Công thức tính độ lệch chuẩn là lấy căn bậc hai của phương sai, cả phương sai và độ lệch chuẩn đều được sử dụng để đo lường sự biến thiên của tập dữ liệu. |
| Ý nghĩa | Sai số chuẩn là một phép đo độ chính xác của một mẫu dữ liệu so với giá trị trung bình của nó. | Độ lệch chuẩn là một phép đo độ biến động hay phân tán của dữ liệu trong một tổng thể. |
| Phụ thuộc vào kích thước mẫu | Có – mẫu càng lớn → SE càng nhỏ | Không |
| Mục đích | Phân tích dữ liệu gốc | Dùng trong kiểm định thống kê, ước lượng trung bình tổng thể |
| Ưu điểm | Được sử dụng để đánh giá độ chính xác của một mẫu dữ liệu | Được sử dụng để đo độ biến động của dữ liệu |
| Nhược điểm | Không phản ánh được độ biến động của toàn bộ dữ liệu | Không phản ánh được độ chính xác của một mẫu dữ liệu |
>> Tham khảo thêm: Dịch vụ thuê làm luận văn theo yêu cầu giảng viên, nhà trường
3. Cách tính sai số chuẩn

Cách tính sai số chuẩn
Sai số chuẩn (Standard Error – SE) được tính dựa trên độ lệch chuẩn (Standard Deviation – SD) và kích thước mẫu (n).
3.1. Các bước tính sai số chuẩn
Quy trình tính gồm hai giai đoạn:
🔹 Giai đoạn 1: Tính độ lệch chuẩn của mẫu
- Bước 1: Tính giá trị trung bình (mean) của mẫu dữ liệu.
- Bước 2: Tính khoảng cách giữa từng giá trị trong mẫu và giá trị trung bình. Khoảng cách này được gọi là sai số (deviation).
- Bước 3: Bình phương khoảng cách (squared deviation) của từng giá trị so với giá trị trung bình.
- Bước 4: Tính trung bình của bình phương khoảng cách từng giá trị so với giá trị trung bình.
- Bước 5: Lấy căn bậc hai của trung bình bình phương khoảng cách để được độ lệch chuẩn (SD).
🔹 Giai đoạn 2: Tính sai số chuẩn
Sau khi có độ lệch chuẩn SD, ta tính sai số chuẩn SE theo công thức: SE = SD / √n
3.2. Ví dụ minh họa
Giả sử đề bài cho một mẫu dữ liệu gồm các giá trị: 4, 6, 8, 10, 12
- Bước 1: Tính giá trị trung bình: (4 + 6 + 8 + 10 + 12) / 5 = 8
- Bước 2: Tính khoảng cách giữa từng giá trị với giá trị trung bình: -4, -2, 0, 2, 4
- Bước 3: Tính bình phương khoảng cách: 16, 4, 0, 4, 16
- Bước 4: Tính trung bình của bình phương khoảng cách: (16 + 4 + 0 + 4 + 16) / 5 = 8
- Bước 5: Lấy căn bậc hai của trung bình bình phương khoảng cách để có độ lệch chuẩn: sqrt(8) = 2.83
- Bước 6: Tính sai số chuẩn: SE = SD / √n = 2.83/ √5 ~ 1.26
⇒ Vậy, sai số chuẩn của mẫu dữ liệu này là 1.26
4. Ứng dụng của sai số chuẩn

Ứng dụng của sai số chuẩn
Sai số chuẩn được sử dụng trong nhiều ứng dụng khác nhau trong lĩnh vực thống kê, bao gồm kiểm định giả thuyết và khoảng tin cậy.
4.1. Sử dụng sai số chuẩn trong kiểm định giả thuyết
Trong thực tiễn phần lớn các bài tập về phân tích dữ liệu, để đánh giá được độ tin cậy của mẫu chúng ta thường sử dụng tham số phương sai, mặt khác dữ liệu này thường không cho sẵn nhưng sai số chuẩn là đại lượng đề bài thường cho, vì thế mọi người cần phải tìm giá trị phương sai dựa theo các thứ tự sau đây:
- Tìm độ lệch chuẩn dựa trên đại lượng sai số chuẩn.
- Tính được phương sai bằng bình phương độ lệch chuẩn.
Ngoài ra, nếu mẫu đó có sai số chuẩn lớn thì sự phân tán của mẫu lớn, dẫn đến độ tin cậy thấp. Ngược lại, mẫu có sai số chuẩn nhỏ thì độ phân tán ít, do đó có độ tin cậy cao hơn.
4.2. Sử dụng sai số chuẩn trong khoảng tin cậy
- Sai số chuẩn được sử dụng trong khoảng tin cậy để tính toán phạm vi có thể chứa giá trị trung bình hoặc tỷ lệ của tổng thể, với một mức độ tin cậy (confidence level) cụ thể.
- Khoảng tin cậy là một công cụ hữu ích để ước tính phạm vi có thể chứa giá trị thực tế của biến số. Khi kích thước mẫu tăng lên, sai số chuẩn giảm, dẫn đến một khoảng tin cậy chính xác hơn cho giá trị trung bình hoặc tỷ lệ của tổng thể.
- Khi chúng ta muốn biết sự khác biệt giữa các nhóm dữ liệu, chúng ta sẽ tiến hành phân tích thống kê bằng cách tìm ra sai số chuẩn của từng nhóm rồi thực hiện so sánh để tìm ra sự đồng nhất giữa các nhóm dữ liệu.
- Nếu giữa các sai số chuẩn của hai nhóm có sự chênh lệch lớn, tức là hai nhóm có sự khác biệt đáng kể, ngược lại nếu các chỉ số tương đương nhau, chúng ta có thể kết luận rằng không có sự khác biệt đáng kể giữa hai nhóm.
5. Các yếu tố ảnh hưởng đến sai số chuẩn

Các yếu tố ảnh hưởng đến sai số chuẩn
Các yếu tố ảnh hưởng đến sai số chuẩn độ bao gồm:
- Phân phối của dữ liệu có ảnh hưởng lớn đến sai số chuẩn.
- Sai số chuẩn sẽ thay đổi tùy thuộc vào phân phối của dữ liệu. Nếu dữ liệu không có phân phối chuẩn thì sai số chuẩn không thể phản ánh chính xác sự phân tán của dữ liệu,
- Kích thước mẫu: Kích thước mẫu càng lớn thì sai số chuẩn càng giảm. Khi kích thước mẫu là vô hạn, sai số chuẩn sẽ tiến tới 0.
- Độ biến thiên của dữ liệu: Nếu dữ liệu có độ biến thiên cao hơn, thì sai số chuẩn sẽ lớn hơn. Ngược lại, nếu độ biến thiên thấp hơn, thì sai số chuẩn sẽ nhỏ hơn.
- Phân phối của dữ liệu: Nếu dữ liệu có phân phối gần chuẩn hoặc chuẩn hơn, thì sai số chuẩn sẽ phù hợp hơn với dữ liệu.
- Sự xuất hiện của các giá trị ngoại lệ: Nếu có các giá trị ngoại lệ trong tập dữ liệu, thì sai số chuẩn có thể bị ảnh hưởng nghiêm trọng, vì nó tính toán bằng cách bình phương sai số của các giá trị so với giá trị trung bình.
- Phương pháp lấy mẫu: Phương pháp lấy mẫu có thể ảnh hưởng đến sai số chuẩn. Nếu phương pháp lấy mẫu được thực hiện ngẫu nhiên và đại diện cho tập dữ liệu gốc, thì sai số chuẩn sẽ phù hợp hơn với dữ liệu.
- Độ chính xác của đo lường: Độ chính xác của đo lường có thể ảnh hưởng đến sai số chuẩn. Nếu độ chính xác của đo lường thấp, thì sai số chuẩn sẽ lớn hơn. Ngược lại, nếu độ chính xác của đo lường cao, thì sai số chuẩn sẽ nhỏ hơn.
- Giá trị ngoại lai (outliers): Giá trị ngoại lai là các giá trị cực đại hoặc cực tiểu trong mẫu dữ liệu. Khi mẫu dữ liệu có giá trị ngoại lai, sai số chuẩn sẽ tăng lên do giá trị trung bình bị ảnh hưởng.
- Cách tính sai số chuẩn: Tùy theo mô hình hoặc kỹ thuật thống kê được sử dụng (ví dụ: hồi quy tuyến tính, bootstrap, hay robust standard error), cách ước lượng sai số chuẩn có thể khác nhau đôi chút. Do đó, cần lựa chọn phương pháp tính phù hợp với đặc điểm dữ liệu và mục tiêu phân tích.
Tóm lại, việc đánh giá chính xác mức độ phân tán của dữ liệu cần phải cân nhắc dựa trên các yếu tố để đảm bảo được sai số chuẩn sẽ tính toán đúng và phù hợp với dữ liệu.
6. Sai lầm phổ biến về sai số chuẩn

Sai lầm phổ biến về sai số chuẩn
Đừng để sai lầm khi tính sai số chuẩn ảnh hưởng đến kết quả đo lường của bạn
6.1. Nhầm lẫn với phương sai
Phương sai là một thước đo cho biết mức độ biến động, phân tán của một biến ngẫu nhiên. Trong khi đó, sai số chuẩn độ lại chỉ là căn bậc hai của phương sai và thể hiện độ lệch chuẩn của giá trị trung bình trong mẫu.
→ Từ đây bạn có thể thấy, hai khái niệm này hoàn toàn khác nhau nên chúng không thể thay thế cho nhau.
6.2. Hiểu sai về sai số chuẩn là thước đo của phân tán mẫu
- Việc xem sai số chuẩn là thước đo của phân tán mẫu là điều hoàn toàn sai lầm.
- Phân tán mẫu là độ lệch của các giá trị dữ liệu so với giá trị trung bình, trong khi sai số chuẩn chỉ là độ lệch chuẩn của giá trị trung bình trong mẫu.
- Chính vì vậy, khi bạn đánh giá sự khác biệt giữa các mẫu, chúng ta cần sử dụng sai số chuẩn để đánh giá độ chính xác của ước lượng nhé!
6.3. Quên không kiểm tra tính đúng đắn của dữ liệu
Trước khi tính toán sai số chuẩn, hãy chắc chắn rằng bạn cần phải kiểm tra tính đúng đắn của dữ liệu trước.
6.4. Không xác định được độ lệch chuẩn
- Để tính toán sai số chuẩn, bạn cần biết độ lệch chuẩn của dữ liệu. Nếu không xác định được độ lệch chuẩn, kết quả tính toán sẽ không chính xác và không đáng tin cậy.
- Khi tính sai số chuẩn cần tránh các sai lầm làm ảnh hưởng đến kết quả
6.5. Không đồng nhất đơn vị đo lường
- Khi tính toán sai số chuẩn, các giá trị dữ liệu phải được đo và đánh giá bằng cùng một đơn vị đo lường.
- Ví dụ: nếu một loạt dữ liệu được đo bằng đơn vị mét cho độ dài và đơn vị giây cho thời gian, khi tính toán tốc độ sẽ phải chuyển đổi các đơn vị đo lường trước khi thực hiện tính toán. Nếu không thực hiện chuyển đổi đơn vị đo lường trước khi tính toán, sẽ dẫn đến sai số trong kết quả tính toán.
7. Lưu ý khi tính và sử dụng sai số chuẩn để đảm bảo độ tin cậy của dữ liệu

Ứng dụng của sai số chuẩn trong các lĩnh vực
7.1. Điều kiện để sử dụng sai số chuẩn
- Xác định giá trị trung bình trước khi tính giá trị sai số chuẩn.
- Sai số chuẩn giúp kết quả được chính xác hơn trong trường hợp thu thập mẫu một cách ngẫu nhiên, khi tính được giá trị trung bình của tổng thể và giá trị thực tế đã biết.
- Khi sử dụng nhiều mẫu, giá trị trung bình có thể thay đổi để tạo ra sự chênh lệch được gọi là sai số chuẩn.
- Nếu giá trị trung bình mẫu bằng với tham số chung thì hàm ước lượng ít khi xảy ra sai số.
- Nếu mẫu thu thập không có số liệu chính xác sẽ không được xác định rõ ràng thông qua các phép đo lường, tuy nhiên nó sẽ được đo chính xác tại điểm chênh lệch giữa giá trị thực của tham số với với giá trị của sai số chuẩn.
7.2. Giới hạn và ứng dụng của sai số chuẩn
Sai số chuẩn của hàm hồi quy có thể sử dụng trong hầu hết các phép tính đo lường và thống kê. Điển hình bạn có thể sử dụng đại lượng này trong các lĩnh vực tính toán chiều cao, cân nặng, đo khối lượng, khảo sát mức độ hài lòng, tính tỷ lệ sản phẩm, nhiệt độ,…
Tuy có thể được áp dụng trong nhiều lĩnh vực khác nhau, nhưng việc sử dụng sai số chuẩn chỉ chính xác khi dữ liệu đáp ứng các giả định cơ bản như phân phối chuẩn, lấy mẫu ngẫu nhiên và không có sai lệch hệ thống.
Tóm lại, sai số chuẩn là một thước đo quan trọng để đánh giá độ biến động và độ phân tán của dữ liệu. Việc hiểu và nắm rõ công thức, các yếu tố ảnh hưởng và 3 sai lầm phổ biến về sai số chuẩn sẽ giúp cho người dùng có cái nhìn tổng quan hơn về mẫu dữ liệu của mình và có thể áp dụng phù hợp các phương pháp kiểm định giả thuyết hoặc khoảng tin cậy.


 14 Tháng 1, 2026
14 Tháng 1, 2026 Share
Share











