Hồi quy tuyến tính là một trong những khái niệm quan trọng nhất trong thống kê, phân tích dữ liệu và máy học. Mặc dù nghe có vẻ phức tạp, hồi quy tuyến tính thực chất là một phương pháp đơn giản nhằm mô hình hóa mối quan hệ giữa các biến. Bài viết dưới đây tổng hợp đầy đủ các nội dung về hồi quy tuyến tính, bao gồm định nghĩa, tầm quan trọng, cách thức hoạt động cùng các loại mô hình hồi quy tuyến tính, dựa trên các dữ liệu và ví dụ được cung cấp trước đó.
1. Hồi quy tuyến tính là gì?
Hồi quy tuyến tính (Linear Regression) là phương pháp thống kê dùng để thiết lập mối quan hệ giữa một biến phụ thuộc (biến mục tiêu) và một hoặc nhiều biến độc lập (biến dự báo) thông qua một phương trình tuyến tính. Mục tiêu của mô hình là tìm ra đường thẳng (hoặc mặt phẳng hay siêu phẳng trong không gian nhiều chiều) phù hợp nhất với dữ liệu.

Khái niệm về hồi quy tuyến tính
Ở dạng đơn giản nhất, mô hình hồi quy tuyến tính được biểu diễn bằng phương trình: y = β₀ + β₁x + ε
Trong đó:
- y: biến phụ thuộc
- x: biến độc lập
- β₀: hệ số chặn
- β₁: hệ số góc
- ε: sai số ngẫu nhiên
Hệ số β₁ cho biết mức độ thay đổi của y khi x thay đổi 1 đơn vị, còn β₀ là giá trị ước lượng của y khi x = 0.
Ví dụ minh họa:
Nếu nghiên cứu mối quan hệ giữa chiều cao và chiều dài bàn chân, mô hình có thể cho ra phương trình:
Chiều cao = 80 + 3.5 × Chiều dài bàn chân
Điều này nghĩa là khi chiều dài bàn chân tăng 1 cm, chiều cao trung bình tăng 3.5 cm.
2. Tại sao hồi quy tuyến tính quan trọng?
Hồi quy tuyến tính được sử dụng rộng rãi không chỉ vì tính đơn giản mà còn vì những lợi ích sau:
2.1. Khả năng dự đoán
Hồi quy tuyến tính có thể dự đoán giá trị của biến phụ thuộc dựa trên các biến độc lập. Ví dụ:
- Dự đoán giá nhà dựa trên diện tích, số phòng ngủ và vị trí
- Dự đoán chi phí dựa trên thu nhập
- Dự đoán sản lượng dựa trên lượng mưa và mức phân bón
2.2. Hiểu rõ mối quan hệ giữa các biến
Thông qua hệ số hồi quy, có thể xác định:
- Biến độc lập nào ảnh hưởng mạnh nhất
- Mức độ ảnh hưởng là tích cực hay tiêu cực
Trong nghiên cứu y khoa, các nhà phân tích có thể dùng hồi quy tuyến tính để xác định yếu tố rủi ro của bệnh như: huyết áp, cholesterol hoặc thói quen hút thuốc.
Tầm quan trọng của hồi quy tuyến tính
2.3. Tính đơn giản và dễ hiểu
Phương trình hồi quy tuyến tính dễ giải thích và trực quan, giúp mô hình phù hợp cho cả người mới bắt đầu lẫn chuyên gia cần lý giải kết quả cho người không chuyên.
2.4. Ứng dụng rộng rãi
Hồi quy tuyến tính xuất hiện trong nhiều lĩnh vực:
- Kinh tế – tài chính
- Kỹ thuật
- Y học
- Khoa học xã hội
- Phân tích dữ liệu và trí tuệ nhân tạo
Theo khảo sát từ KDnuggets, hồi quy tuyến tính nằm trong ba phương pháp phân tích được dùng nhiều nhất.
2.5. Nền tảng cho các phương pháp nâng cao
Nhiều thuật toán máy học phức tạp được xây dựng trên khung hồi quy tuyến tính, chẳng hạn:
- Hồi quy logistic
- Hồi quy đa thức
- Ridge, Lasso
- Generalized Linear Models (GLMs)
- Mạng nơ-ron
3. Hồi quy tuyến tính hoạt động như thế nào?
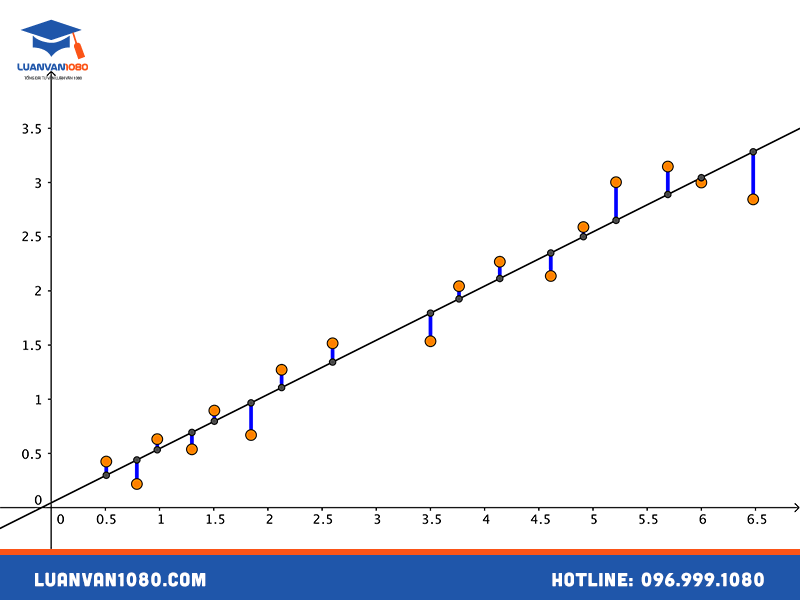
Hồi quy tuyến tính hoạt động bằng cách tìm ra một đường thẳng phù hợp nhất với tập dữ liệu sao cho tổng bình phương sai số là nhỏ nhất. Đây chính là cơ chế của phương pháp Ordinary Least Squares (OLS).
3.1. Phương trình mô hình
Mối quan hệ giữa hai biến X và Y được mô tả bởi đường thẳng:
Y = β₀ + β₁X + ε
Ý nghĩa:
- β₁: lượng thay đổi trong Y khi X tăng 1 đơn vị
- β₀: giá trị Y khi X bằng 0 (dù đôi khi không có ý nghĩa thực tế)
3.2. OLS – Phương pháp bình phương tối thiểu
OLS tìm các hệ số β sao cho tổng bình phương sai số giữa giá trị thực và giá trị dự đoán là nhỏ nhất. Sai số được tính bằng:
Sai số = Giá trị thực – Giá trị dự đoán
3.3. Ví dụ minh họa cách tính β₀ và β₁
Dựa trên công thức:
- β₁ = r × (σy / σx)
- β₀ = mean(y) – β₁ × mean(x)
Với dữ liệu đã cho, tính được:
- β₁ = 2.64
- β₀ = –2.2
Phương trình hồi quy:
- Y = –2.2 + 2.64 × X
4. Các giả định của hồi quy tuyến tính
Để mô hình đạt kết quả chính xác, dữ liệu cần thỏa các giả định:
- Tuyến tính và tính cộng thêm: Quan hệ giữa biến phụ thuộc và độc lập phải là tuyến tính. Ảnh hưởng của từng biến độc lập lên biến phụ thuộc là cộng thêm.
- Tính bình thường của sai số: Sai số (phần dư) nên phân bố chuẩn. Có thể kiểm tra bằng biểu đồ Q–Q.
- Phương sai không đổi: Sai số cần có độ lệch chuẩn không đổi trên toàn bộ dải giá trị của biến độc lập.
- Sự độc lập của sai số: Phần dư không được tương quan lẫn nhau. Ví dụ: trong dữ liệu chuỗi thời gian, không được để sai số của thời điểm này phụ thuộc vào thời điểm trước.
- Vấn đề đa cộng tuyến: Trong hồi quy đa biến, nếu các biến độc lập tương quan mạnh với nhau, kết quả hồi quy có thể không ổn định.
>> Đọc thêm: Phương sai và độ lệch chuẩn có khác nhau không?
5. Hồi quy tuyến tính trong máy học
Trong Machine Learning, hồi quy tuyến tính là thuật toán học có giám sát dùng để dự đoán biến mục tiêu liên tục. Thuật toán học bằng cách tối ưu hóa hàm mất mát, thường là tổng bình phương sai số.
5.1. Quy trình hoạt động
Chuẩn bị dữ liệu
Làm sạch dữ liệu, xử lý giá trị thiếu, chuẩn hóa nếu cần.
Chọn mô hình
- Hồi quy tuyến tính đơn biến
- Hồi quy tuyến tính đa biến
Huấn luyện mô hình
Tìm các hệ số β₀, β₁,… sao cho hàm mất mát nhỏ nhất.
Có thể dùng:
- Phương pháp bình phương tối thiểu OLS
- Gradient Descent
Đánh giá mô hình
Dùng dữ liệu kiểm tra để đánh giá khả năng tổng quát hóa của mô hình.
Dự đoán
Sử dụng phương trình hồi quy để dự đoán giá trị Y mới.

Hồi quy tuyến tính trong máy học
5.2. Ví dụ minh họa
Giả sử dự đoán giá nhà dựa trên diện tích:
- Chia dữ liệu thành tập huấn luyện và kiểm tra
- Mô hình học phương trình: Giá nhà = β₀ + β₁ × Diện tích
- Áp dụng phương trình để dự đoán các căn nhà mới và so sánh với giá thật
6. Các loại hồi quy tuyến tính
6.1. Hồi quy tuyến tính đơn biến
Có một biến độc lập và một biến phụ thuộc.
Ví dụ: Điểm thi = β₀ + β₁ × Số giờ học + ε
6.2. Hồi quy tuyến tính đa biến
Có nhiều biến độc lập.
Ví dụ: Giá nhà = β₀ + β₁ × Diện tích + β₂ × Số phòng ngủ + β₃ × Khoảng cách + ε
Hồi quy đa biến là mở rộng của hồi quy đơn biến.
6.3. Hồi quy tuyến tính tổng quát
GLM là họ mô hình mở rộng từ hồi quy tuyến tính.
Ví dụ: Hồi quy Logistic là một GLM, được dùng cho bài toán phân loại, không phải dự đoán giá trị liên tục.
>> Tham khảo thêm: Giá làm luận văn chi phí phải chăng, đáng tin cậy
7. Ví dụ tính toán hồi quy tuyến tính
Để hiểu rõ hơn về phương pháp bình phương nhỏ nhất trong hồi quy tuyến tính, chúng ta sẽ xem xét một ví dụ đơn giản về bài toán dự đoán giá nhà dựa trên diện tích. Giả sử chúng ta có bộ dữ liệu gồm 10 căn nhà với diện tích và giá tương ứng như sau:
| Diện tích (m²) | Giá (tỷ VNĐ) |
| 50 | 1.5 |
| 80 | 2.3 |
| 65 | 2 |
| 120 | 3.5 |
| 90 | 2.8 |
| 75 | 2.1 |
| 100 | 3 |
| 60 | 2 |
| 110 | 3.3 |
| 85 | 2.4 |
Mục tiêu: Dự đoán giá của một căn nhà có diện tích 95m² bằng cách sử dụng phương pháp bình phương nhỏ nhất để xây dựng mô hình hồi quy tuyến tính.
Các bước thực hiện:
Tính toán các giá trị trung bình:
- Trung bình diện tích (x̄) = (50 + 80 + … + 85) / 10 = 83
- Trung bình giá nhà (ȳ) = (1.5 + 2.3 + … + 2.4) / 10 = 2.49
Tính toán các độ lệch và tổng cần thiết:
- Σ(x – x̄)² = (50-83)² + (80-83)² + … + (85-83)² = 3560
- Σ(x – x̄)(y – ȳ) = (50-83)(1.5-2.49) + (80-83)(2.3-2.49) + … + (85-83)(2.4-2.49) = 119.3
Tính toán hệ số hồi quy:
- β1 = Σ(x – x̄)(y – ȳ) / Σ(x – x̄)² = 119.3 / 3560 ≈ 0.0335
- β0 = ȳ – β1 * x̄ = 2.49 – 0.0335 * 83 ≈ -0.2805
Xây dựng phương trình hồi quy: y = β0 + β1 * x = -0.2805 + 0.0335 * x
Dự đoán giá nhà: Với x = 95, ta có y = -0.2805 + 0.0335 * 95 ≈ 2.852 tỷ VNĐ
Kết luận: Mô hình hồi quy tuyến tính dự đoán rằng căn nhà có diện tích 95m² sẽ có giá khoảng 2.852 tỷ đồng.
Hồi quy tuyến tính là một phương pháp thống kê và thuật toán máy học nền tảng, được sử dụng rộng rãi để dự đoán và phân tích mối quan hệ giữa các biến. Với tính đơn giản, trực quan và hiệu quả, nắm vững hồi quy tuyến tính không chỉ giúp hiểu sâu dữ liệu mà còn mở đường đến các phương pháp phân tích và mô hình hóa nâng cao hơn trong khoa học dữ liệu và trí tuệ nhân tạo.


 14 Tháng 1, 2026
14 Tháng 1, 2026 Share
Share










