Ở bài viết này, Luận văn 1080 sẽ phân tích sâu về vấn đề hiện tượng đa cộng tuyến là gì, phương pháp phân tích, những nguyên tắc, quy trình cũng như một số vấn đề cần lưu ý khi phân tích đa cộng tuyến trong kinh tế lượng. Cùng bắt đầu tìm hiểu ngay bên dưới nhé!

Đa cộng tuyến(multicollinearity) là gì?
1. Bản chất của đa cộng tuyến(multicollinearity)
1.1. Định nghĩa
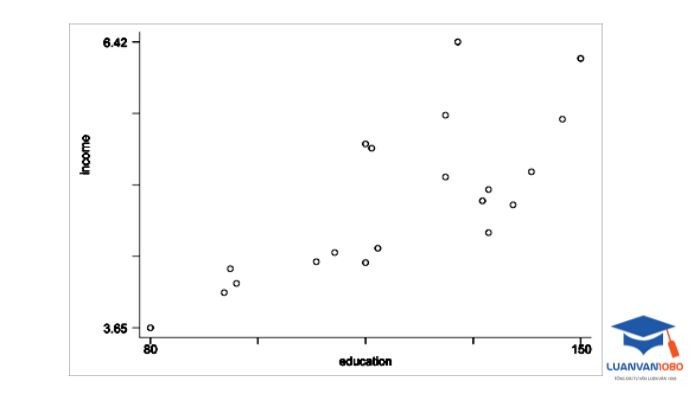
Hiện tượng đa cộng tuyến là gì?
- Đa cộng tuyến (Multicollinearity) là hiện tượng phân tích hồi quy tuyến tính (Linear Regression Analysis) trong thống kê khi hai hoặc nhiều biến độc lập(Independent Variables) trong một mô hình tuyến tính có mối quan hệ tuyến tính mạnh với nhau.
- Nó dẫn đến việc giảm độ chính xác của mô hình và làm tăng sai số trong dự đoán(p-value), cũng như làm giảm khả năng kiểm định sự ảnh hưởng của từng biến độc lập đối với biến phụ thuộc.
- Hiện tượng đa cộng tuyến gồm 2 thành phần chính: đa cộng tuyến hoàn toàn(Perfect Multicollinearity) và đa cộng tuyến không hoàn toàn(Imperfect Multicollinearity).
>> Đọc thêm: Chi square là gì? Các bước chạy kiểm định chi square trong spss
1.2. Ý nghĩa
- Đa cộng tuyến là một trong những vấn đề thường gặp trong phân tích thống kê. Việc xác định và khắc phục đa cộng tuyến là rất quan trọng để đảm bảo tính chính xác và đáng tin cậy của kết quả phân tích.
- Nếu không xử lý, đa cộng tuyến sẽ làm tăng sai số chuẩn (Standard Error) của các hệ số hồi quy, giảm mức ý nghĩa thống kê (Statistical Significance) và gây khó khăn khi đánh giá ảnh hưởng của từng biến độc lập lên biến phụ thuộc.
- Do đó, việc kiểm tra và khắc phục đa cộng tuyến là bước quan trọng trong quy trình phân tích hồi quy để đảm bảo kết quả có giá trị thực tiễn và độ tin cậy cao.
⇒ Vì vậy, việc xác định và khắc phục đa cộng tuyến rất quan trọng nhằm đảm bảo tính chính xác và tính đáng tin cậy của kết quả phân tích.
1.3. Vai trò của đa cộng tuyến trong phân tích thống kê
- Đa cộng tuyến là hiện tượng phổ biến trong phân tích thống kê, đặc biệt là trong mô hình hồi quy tuyến tính. Nếu không xử lý tốt đa cộng tuyến, kết quả phân tích sẽ bị sai lệch và không chính xác.
- Đa cộng tuyến trong SPSS ảnh hưởng đến tính chất của các hệ số hồi quy, làm tăng sai số chuẩn và tăng nguy cơ xảy ra hiện tượng giả hồi quy.
- Đa cộng tuyến còn ảnh hưởng đến độ chính xác của dự báo và khả năng giải thích mô hình.
2. Nguyên nhân gây ra hiện tượng đa cộng tuyến
Nguyên nhân gây ra hiện tượng đa cộng tuyến
2.1. Mối quan hệ tuyến tính giữa các biến
Mối quan hệ tuyến tính mạnh giữa các biến đầu vào trong mô hình tuyến tính có thể gây ra hiện tượng đa cộng tuyến. Vì nếu hai biến đầu vào có mối quan hệ tuyến tính mạnh, thì khi một trong hai biến thay đổi, biến còn lại cũng sẽ thay đổi theo.
→ Do đó, việc phân biệt được ảnh hưởng của từng biến đến biến phụ thuộc trở nên khó khăn.
Ví dụ: chúng ta muốn xây dựng một mô hình để dự đoán giá nhà dựa trên các yếu tố như diện tích, số phòng ngủ và vị trí của căn nhà.
- Nếu ta đưa vào cả hai biến “diện tích” và “số phòng ngủ”, hai biến này thường có mối quan hệ tuyến tính, có nghĩa là diện tích của căn nhà sẽ tăng theo cấp số nhân khi số phòng ngủ tăng. Trường hợp này, mô hình của chúng ta sẽ gặp phải vấn đề đa cộng tuyến.
- Để giải quyết vấn đề này, chúng ta có thể loại bỏ một trong hai biến để tránh mối quan hệ tuyến tính giữa chúng.
>> Tham khảo thêm: Dịch vụ thuê làm luận văn đáng tin cậy với hợp đồng minh bạch
2.2. Sử dụng quá nhiều biến độc lập sự tương quan mạnh với nhau trong một mô hình tuyến tính
Khi có sự tương quan mạnh giữa các biến độc lập trong mô hình, chúng ta sẽ gặp phải hiện tượng đa cộng tuyến trong SPSS. Khi các biến độc lập có mối quan hệ mạnh với nhau, chúng có thể giải thích một phần lớn phương sai của các biến phụ thuộc, dẫn đến sự mất đi tính duy nhất của việc ước lượng hệ số. Điều này gây khó khăn cho việc đánh giá độ ảnh hưởng của mỗi biến độc lập trên biến phụ thuộc, và làm giảm độ chính xác của kết quả dự báo của mô hình.
- Ví dụ 1: trong mô hình dự đoán lương của nhân viên, nếu một số nhân viên có chức vụ cao và đồng thời có nhiều năm kinh nghiệm, thì cả hai biến này đều có tác động đến lương của nhân viên, dẫn đến sự trùng hợp trong dữ liệu thu thập và ảnh hưởng đến kết quả của mô hình.
- Ví dụ 2: nếu chúng ta xây dựng mô hình dự đoán giá nhà dựa trên diện tích và số phòng, thì rất có thể các biến này có sự tương quan mạnh. Khi đó, một biến có thể được giải thích bằng biến còn lại, dẫn đến mô hình không có tính độc lập giữa các biến.
→ Tóm lại: Việc phát hiện và giải quyết đa cộng tuyến là rất quan trọng trong phân tích thống kê, bởi vì nó có thể làm sai lệch kết quả và dẫn đến các dự đoán không chính xác.
3. Cách phát hiện đa cộng tuyến trong SPSS
Để phát hiện hiện tượng đa cộng tuyến trong SPSS, có thể sử dụng các phương pháp sau:
3.1. Ma trận tương quan
Sử dụng ma trận tương quan để phát hiện đa cộng tuyến
- Ma trận tương quan là ma trận bao gồm các hệ số tương quan giữa các cặp biến trong dữ liệu. Việc kiểm tra tương quan giữa các biến trong dữ liệu bằng cách tính ma trận tương quan rất quan trọng để phát hiện được hiện tượng đa cộng tuyến.
- Cụ thể, nếu một số cặp biến có tương quan cao (thông thường được định nghĩa là hệ số tương quan lớn hơn 0,7), thì đó là một dấu hiệu cho thấy có thể có đa cộng tuyến trong dữ liệu, cần phải xem xét và xử lý đa cộng tuyến trước khi sử dụng chúng trong mô hình tuyến tính khác.
3.2. Hệ số phóng đại phương sai (VIF)
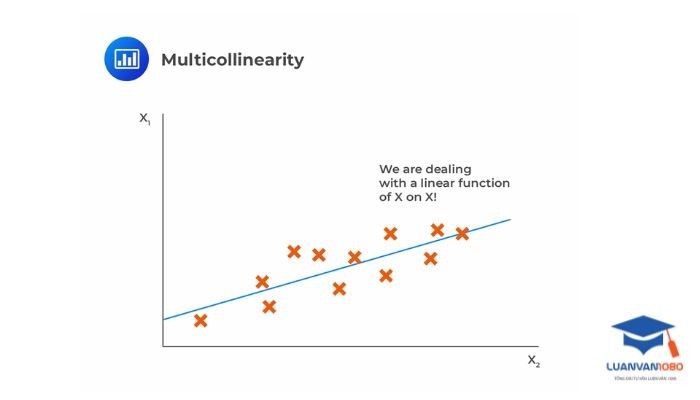
Cách phát hiện đa cộng tuyến bằng Hệ số phóng đại phương sai (VIF)
- Hệ số phóng đại phương sai (VIF) là một chỉ số được sử dụng để đánh giá mức độ đa cộng tuyến giữa một biến và các biến khác trong một mô hình tuyến tính. VIF sẽ được tính bằng cách so sánh phương sai của hệ số ước lượng một biến với phương sai của mô hình tuyến tính gồm các biến khác.
- Thông thường một giá trị VIF lớn hơn 10 sẽ là dấu hiệu cho thấy mô hình này có xuất hiện đa cộng tuyến. Tức là, giá trị VIF càng lớn thì mức độ đa cộng tuyến càng cao.
Lưu ý: Tuy nhiên, việc kiểm định đa cộng tuyến còn tùy thuộc vào ngữ cảnh và mục đích của việc phân tích mà giá trị của ngưỡng này có thể khác nhau.
Thông qua việc tính giá trị phóng đại phương sai VIF cho từng biến dự đoán, bạn sẽ biết được các biến độc lập trong mô hình hồi hồi quy có tương quan mạnh với nhau hay không.
3.3. Kiểm tra độc lập tuyến tính
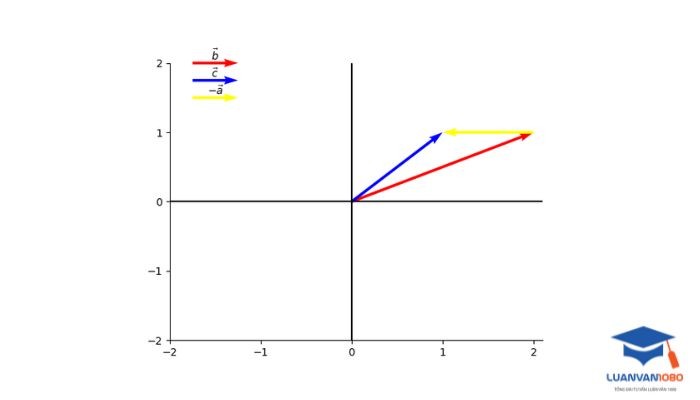
Phát hiện đa cộng tuyến bằng cách sử dụng kiểm tra độc lập tuyến tính
- Trong một mô hình tuyến tính đơn giản, mỗi biến độc lập đóng vai trò như một độc lập tuyến tính, có thể ảnh hưởng tới biến phụ thuộc theo một cách tuyến tính.
- Để kiểm tra độc lập tuyến tính của một biến, bạn có thể sử dụng phương pháp kiểm tra hình dạng phân bổ của biến hoặc kiểm tra phương sai.
- Nếu một biến có phương sai gần bằng 0, hoặc nếu phân bố của nó có hình dạng không tuyến tính, thì có thể nó sẽ không đóng góp nhiều vào mô hình và có thể bị loại bỏ.
- Nếu một biến không độc lập tuyến tính sẽ ảnh hưởng đến độ chính xác của mô hình, từ đó dẫn tới các dự đoán không có tính chính xác cao.
3.4. Kiểm tra tương quan bội
- Nếu một mô hình có các biến độc lập có tương quan bội, thì nó có thể dẫn đến đa cộng tuyến. Kiểm tra tương quan bội giữa các biến độc lập có thể giúp phát hiện các biến này.
- Để kiểm tra tương quan bội giữa các biến độc lập, bạn có thể sử dụng phương pháp PCA (giải thích phương sai) hoặc ma trận tương quan.
- Nếu các biến độc lập có tương quan bội, bạn có thể dễ dàng giảm thiểu đa cộng tuyến bằng cách kết hợp hoặc loại bỏ một số biến.
4. Cách khắc phục hiện tượng đa cộng tuyến
Hướng dẫn cách khắc phục đa cộng tuyến
Để khắc phục hiện tượng đa cộng tuyến, ta có thể áp dụng một số giải pháp như sau:
4.1. Loại bỏ biến độc lập
- Ưu điểm: Đơn giản và dễ thực hiện.
- Nhược điểm: Có thể gây mất mát thông tin quan trọng. Nếu loại bỏ biến có ảnh hưởng thực sự đến biến phụ thuộc, sẽ làm giảm tính chính xác của mô hình.
4.2. Kết hợp các biến để tạo ra các biến mới
- Ưu điểm: Giảm đáng kể hiện tượng đa cộng tuyến và giúp tăng tính chính xác của mô hình.
- Nhược điểm: Không phải lúc nào cũng thể hiện được quan hệ giữa các biến. Đôi khi kết hợp các biến có thể làm giảm tính giải thích của mô hình, việc kết hợp các biến có thể dẫn đến mất mát thông tin và làm giảm độ chính xác của mô hình.
4.3. Sử dụng phương pháp phân tích thành phần chính (PCA)
- Ưu điểm: Khắc phục hiện tượng đa cộng tuyến một cách hiệu quả. PCA có thể giảm số lượng biến và giúp giảm nhiễu và giảm thời gian tính toán.
- Nhược điểm: Không giải thích được ý nghĩa của các biến được giải thích bằng các thành phần chính, do đó không phù hợp cho các nghiên cứu có tính giải thích cao.
4.4. Giảm giá trị hệ số phóng đại phương sai (VIF)
- Ưu điểm: Đánh giá mức độ đa cộng tuyến giữa các biến và giúp xác định các biến cần được loại bỏ.
- Nhược điểm: Chỉ đánh giá đa cộng tuyến giữa từng cặp biến, không đánh giá tác động của toàn bộ các biến lên nhau. Điều này có thể dẫn đến việc giữ lại các biến dẫn đến đa cộng tuyến trong mô hình.
4.5. Sử dụng mô hình không tuyến tính
- Ưu điểm: Có thể khắc phục hiện tượng đa cộng tuyến khi sử dụng mô hình không tuyến tính như mô hình rừng ngẫu nhiên, mô hình xgboost,…
- Nhược điểm: Mô hình không tuyến tính thường phức tạp hơn mô hình tuyến tính và khó khăn trong diễn giải kết quả, dễ gây overfitting, khó khăn trong việc xác định các biến độc lập quan trọng, không phản ánh được quan hệ tuyến tính giữa biến
Thông tin thêm: Đa cộng tuyến và kiểm định Kruskal-Wallis có mối quan hệ mật thiết trong việc kiểm tra sự khác biệt giữa các nhóm dữ liệu. Nếu dữ liệu của chúng ta bị ảnh hưởng bởi đa cộng tuyến, thì kiểm định Kruskal-Wallis có thể không chính xác.
5. Ứng dụng việc phân tích đa cộng tuyến trong các lĩnh vực
Ứng dụng việc phân tích đa cộng tuyến trong các lĩnh vực
5.1. Y học
Đa cộng tuyến có thể ảnh hưởng đến kết quả của các nghiên cứu y học, khi các yếu tố có liên quan đến sức khỏe (như thuốc, chế độ ăn uống và các yếu tố môi trường khác) đồng thời ảnh hưởng đến nhau.
5.2. Kinh tế học
Trong kinh tế học, đa cộng tuyến có thể xuất hiện khi các yếu tố kinh tế (như thu nhập, giá cả và chính sách kinh tế) ảnh hưởng đến nhau và làm khó khăn cho việc dự báo và mô hình hóa tác động của các yếu tố này.
5.3. Khoa học xã hội
Trong các lĩnh vực như tâm lý học, xã hội học, và giáo dục, đa cộng tuyến có thể xuất hiện khi các yếu tố như trình độ học vấn, độ tuổi, và nghề nghiệp có tác động đồng thời lên nhau và ảnh hưởng đến các kết quả nghiên cứu.
5.4. Khoa học môi trường
Trong các lĩnh vực như khoa học môi trường, đa cộng tuyến có thể xuất hiện khi các yếu tố về môi trường (như nhiệt độ, độ ẩm, độ ô nhiễm) đồng thời ảnh hưởng đến các chỉ số môi trường khác.
Phân tích định lượng trong SPSS cũng gây rất nhiều khó khăn cho các bạn sinh viên và các nhà nghiên cứu. Đặc biệt khi bạn không nhiều kinh nghiệm và kỹ năng thực hiện phân tích định lượng thì lựa chọn dịch vụ chạy SPSS thuê là điều rất cần thiết trong trường hợp này. Liên hệ ngay với Luận văn 1080 khi bạn cần sự trợ giúp. Với đội ngũ chuyên gia nhiều kinh nghiệm, chúng tôi cam kết mang đến cho bạn kết quả nghiên cứu tốt nhất.
Hy vọng bài viết về đa cộng tuyến là gì phía trên, Luận Văn 1080 đã giúp bạn cập nhật được nhiều kiến thức bổ ích. Nắm rõ quy trình để khắc phục đa cộng tuyến và kiểm định đa cộng tuyến sẽ giúp bạn thực hiện tốt bài luận của mình.


 14 Tháng 1, 2026
14 Tháng 1, 2026 Share
Share











